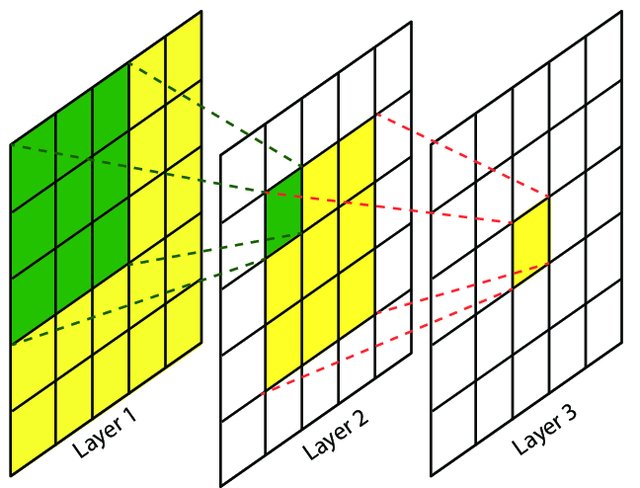
线性回归
一句话表示,就是数据的分布是按照如下的线性表达式:
$$
y=w_1x_1+w_2x_2+...+w_nx_n+b
$$
$w_n$就是网络的权重(参数),b 也是一种权重。
代码实现
import random
import torch
from d2l import torch as d2l
def synthetic_data(w, b, num_examples):
X = torch.normal(0, 1, (num_examples, len(w)))
y = torch.matmul(X, w) + b
y += torch.normal(0, 0.01, y.shape)
return X, y.reshape(-1, 1)
true_w = torch.tensor([2, -3.4])
true_b = 4.2
features, labels = synthetic_data(true_w, true_b, 1000)
features.shape, labels.shape
(torch.Size([1000, 2]), torch.Size([1000, 1]))
def data_iter(batch_size,features,labels):
num_examples=len(features)
indices=list(range(num_examples))
random.shuffle(indices)
for i in range(0,num_examples,batch_size):
batch_indices=torch.tensor(indices[i:min(i+batch_size,num_examples)])
yield features[batch_indices],labels[batch_indices]
batch_size=10
for X,y in data_iter(batch_size,features,labels):
print(X,'\n',y)
break
tensor([[-1.2750, 1.5482],
[-0.0563, -2.0593],
[-0.3648, -0.0083],
[ 0.2933, 0.3219],
[-0.6043, -0.0551],
[-1.1544, -0.0258],
[ 0.9690, -0.7872],
[ 0.7860, 0.0937],
[ 0.9102, -0.6743],
[ 1.6593, 0.3044]])
tensor([[-3.5984],
[11.0968],
[ 3.5161],
[ 3.6972],
[ 3.1954],
[ 1.9791],
[ 8.8084],
[ 5.4522],
[ 8.3228],
[ 6.4840]])
w = torch.normal(0, 0.01, size=(2, 1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)
def linreg(X, w, b):
return torch.matmul(X, w) + b
def squared_loss(y_hat, y):
return (y_hat - y.reshape(y_hat.shape))**2/2
def sgd(params, lr, batch_size):
with torch.no_grad():
for param in params:
param -= lr * param.grad / batch_size
param.grad.zero_()
lr = 0.03
num_epochs = 3
net = linreg
loss = squared_loss
for epoch in range(num_epochs):
for X, y in data_iter(batch_size, features, labels):
l = loss(net(X, w, b), y)
l.sum().backward()
sgd([w, b], lr, batch_size)
with torch.no_grad():
train_l = loss(net(features, w, b), labels)
print(f'open {epoch+1}, loss {float(train_l.mean())}')
open 1, loss 5.805317050544545e-05
open 2, loss 5.791278090327978e-05
open 3, loss 5.7983954320661724e-05
print(f'w的估计误差:{true_w-w.reshape(true_w.shape)}')
print(f'b的估计误差:{true_b-b}')
w的估计误差:tensor([-2.5511e-05, -1.8573e-04], grad_fn=<SubBackward0>)
b的估计误差:tensor([0.0001], grad_fn=<RsubBackward1>)
文字说明
所有深度学习训练过程都可以用四个步骤概括:1.前向传播(输入到网络),2.计算损失(损失函数可导,且损失函数的值必须是标量),3.计算梯度(用于下一步的更新参数。backward()),4.更新网络参数(这里用的是 SGD)
SGD
gpt:
随机梯度下降(Stochastic Gradient Descent,SGD)是一种常用的优化算法,常用于机器学习中的参数优化问题。在传统的梯度下降算法中,每次更新模型参数需要遍历整个训练集,计算所有样本的梯度平均值,这样的计算代价很大,尤其是在大规模数据集上。SGD 算法通过每次从训练集中随机选择一个样本进行梯度计算和模型参数更新,降低了计算代价,加快了模型收敛速度。此外,SGD 还可以避免陷入局部最优解,使得模型更有可能达到全局最优解。
然而,SGD 也有一些缺点,如对于数据的噪声敏感、容易受到初始点的影响等。因此,在实践中,常常使用一些改进的 SGD 算法,如动量优化、Adagrad、Adam 等来克服这些缺点。
这段话里面。SGD 每次应该不一定只选择一个样本,而是若干个样本。这也因此引入了 batch_size 的概念。batch_size 就是每次计算梯度时选取样本的数量。