4 篇博文含有标签「machine-learning」

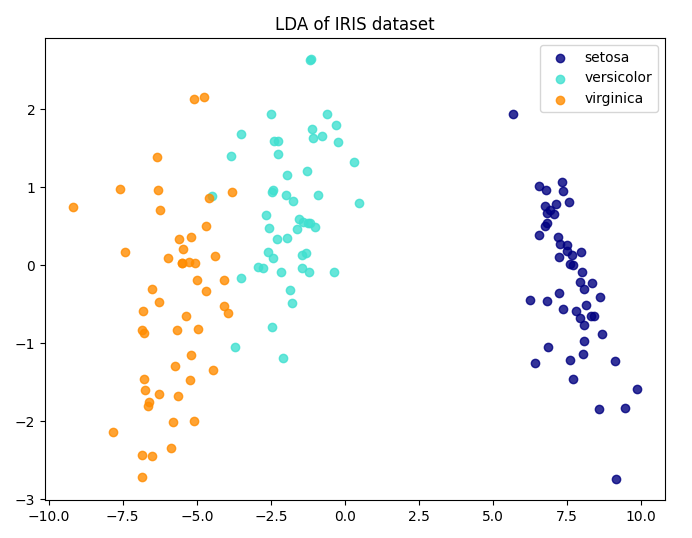
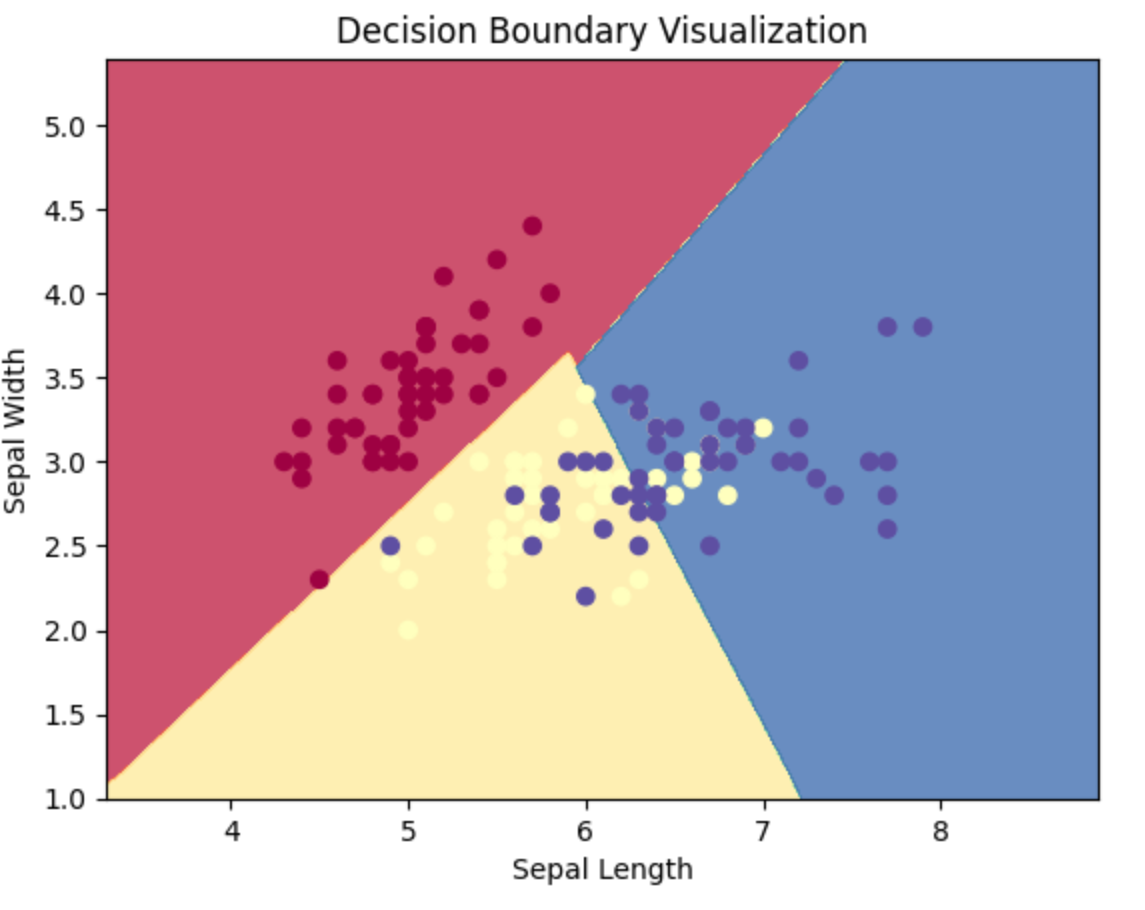
python机器学习-模型评估与参数调优

2023年10月23日 · 阅读需 3 分钟

Jason Lee

性能指标（二分类问题）

混淆矩阵

首先，为什么在有准确率（accuracy）的情况下，还要引入别的指标呢？因为受困于数据收集的客观限制，容易出现不平衡问题，比如正类的数量远远大于负类。这样，即使模型将所有样本预测为正类，损失函数也很低，达到了欺骗的效果。因此，我们需要将正类和负类分别的预测结果列出来，如混淆矩阵。

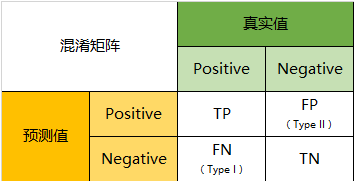
准确率和召回率

基于混淆矩阵，得到了准确率（precision）和召回率（recall）：

precision = TP/(TP+FP)
recall = TP/(TP+FN)

ROC 曲线

我们通过真正率（TPR）和假真率（FPR）来衡量分类器的性能。

通过 ROC 空间，我们明白了一条 ROC 曲线其实代表了无数个分类器。那么我们为什么常常用一条 ROC 曲线来描述一个分类器呢？仔细观察 ROC 曲线，发现其都是上升的曲线（斜率大于 0），且都通过点（0,0）和点（1,1）。其实，这些点代表着一个分类器在不同阈值下的分类效果，具体的，曲线从左往右可以认为是阈值从 0 到 1 的变化过程。当分类器阈值为 0，代表不加以识别全部判断为 0，此时 TP=FP=0，TPR=TP/P=0，FPR=FP/N=0；当分类器阈值为 1，代表不加以识别全部判断为 1，此时 FN=TN=0，P=TP+FN=TP, TPR=TP/P=1，N=FP+TN=FP, FPR=FP/N=1。所以，ROC 曲线描述的其实是分类器性能随着分类器阈值的变化而变化的过程。对于 ROC 曲线，一个重要的特征是它的面积，面积为 0.5 为随机分类，识别能力为 0，面积越接近于 1 识别能力越强，面积等于 1 为完全识别。

python机器学习-数据降维

2023年10月15日 · 阅读需 6 分钟

Jason Lee

PCA（主成分分析）

example:

import numpy as np
from sklearn.decomposition import PCA

# 创建一个示例数据集
data = np.array([
    [1.5, 2.0, 3.0, 4.5],
    [2.2, 2.8, 3.9, 4.2],
    [1.9, 2.5, 3.2, 4.7],
    [2.7, 3.0, 3.6, 4.0],
    [2.3, 2.9, 3.7, 4.3]
])

# 初始化 PCA 模型，指定主成分的数量
pca = PCA(n_components=2)

# 对数据进行拟合
pca.fit(data)

# 获取主成分
principal_components = pca.components_

# 获取主成分的方差贡献比例
explained_variance_ratio = pca.explained_variance_ratio_

# 对数据进行 PCA 转换
transformed_data = pca.transform(data)

print("原始数据：\n", data)
print("主成分：\n", principal_components)
print("主成分的方差贡献比例：", explained_variance_ratio)
print("PCA 转换后的数据：\n", transformed_data)

输出：

原始数据：
 [[1.5 2.  3.  4.5]
 [2.2 2.8 3.9 4.2]
 [1.9 2.5 3.2 4.7]
 [2.7 3.  3.6 4. ]
 [2.3 2.9 3.7 4.3]]
主成分：
 [[-0.61305201 -0.55633419 -0.46392272  0.31533349]
 [-0.53989171 -0.03347232  0.83292811  0.11673604]]
主成分的方差贡献比例： [0.87919714 0.0703791 ]
PCA 转换后的数据：
 [[ 1.00928239 -0.02497259]
 [-0.37705186  0.28493986]
 [ 0.45617665 -0.0677326 ]
 [-0.71873459 -0.2649261 ]
 [-0.36967259  0.07269143]]

在深入之前，有必要解释一下 PCA 为什么在高维数据中找最大方差的方向而不是别的指标（比如最大值），来降维的？找到最大方差的方向意味着在这个方向上数据的变化最为显著，即信息越丰富。以我之前接触到的人脸图像为例，不同位置的像素有差异，才能让分类器有能力识别。

为了将我视频学习到的和这个例子对应起来，将输出中的几个部分进行解释：

首先，这个例子中的原始数据是有五个样本，每个样本有四个维度的特征（一开始我还真没搞明白这个）。然后，pca 算法找出四个主成分（找的过程是通过计算协方差矩阵和特征向量等步骤得来的，视频举的例子是几何平面便于理解，而书上的公式是一种通用的方法，适合任意数量纬度特征，二者本质相同），也就是输出中的主成分。主成分本质上是一个方向向量，且模为 1，所以本例中的主成分有两组，每组四个值，对应四种特征，哪个特征的绝对值最大，说明哪个特征在这个主成分中占主导。方差贡献比例就是，依次计算所有数据在某一主成分上的投影点到距离之和，然后全部求和，最后计算一个主成分所占的比例，比例越高，说明方差越大，数据在这个主成分上差异越明显。最后的转换后数据，则是将所有数据在某一主成分上的投影点到距离，作为以各主成分为新坐标轴的空间内的坐标。

LDA（线性判别分析）

不同于 PCA，LDA 有类别标签参与训练，所以是有监督的。LDA 训练过程中的优化目标也变成了最大化不同类之间的类间差距，而不是 PCA 的找样本内方差最大的方向，可以说是完全不同的方法，但是都能实现降维。

LDA 在一条线上投影数据点，并且让投影点的不同类之间的均值差距最大，而同类的方差最小，这样就让不同类之间的类间差距最大化。

可以说，LDA 的适用范围更窄些，它要求数据有明确的标签，且只适用分类问题；而 PCA 则适用范围更广，因为它只要求提供特征，能适用于不限于分类的问题。

example:

# 导入必要的库
from sklearn import datasets
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
import matplotlib.pyplot as plt

# 加载示例数据集（这里以Iris数据集为例）
iris = datasets.load_iris()
X = iris.data
y = iris.target

# 创建LDA模型
lda = LinearDiscriminantAnalysis(n_components=2)  # 我们希望将数据降至二维

# 拟合模型并进行降维
X_lda = lda.fit_transform(X, y)

# 绘制降维后的数据
plt.figure(figsize=(8, 6))
colors = ['navy', 'turquoise', 'darkorange']
lw = 2

for color, i, target_name in zip(colors, [0, 1, 2], iris.target_names):
    plt.scatter(X_lda[y == i, 0], X_lda[y == i, 1], alpha=0.8, color=color,
                label=target_name)
plt.legend(loc='best', shadow=False, scatterpoints=1)
plt.title('LDA of IRIS dataset')
plt.show()

《python 机器学习》数据预处理

2023年10月10日 · 阅读需 3 分钟

Jason Lee

缺失数据值的处理

在 scikit-learn 中处理缺失数据的方法：

SimpleImputer: SimpleImputer 是 scikit-learn 中用于填充缺失数据的类。你可以使用不同的策略来填充缺失值，包括均值、中位数、众数等。例如：

from sklearn.impute import SimpleImputer

imputer = SimpleImputer(strategy='mean')  # 使用均值填充缺失值
X_imputed = imputer.fit_transform(X)

KNNImputer: KNNImputer 使用 K-最近邻算法来填充缺失值，根据相邻样本的值进行估计。

from sklearn.impute import KNNImputer

imputer = KNNImputer(n_neighbors=5)  # 使用5个最近邻的值来估计缺失值
X_imputed = imputer.fit_transform(X)

在 pandas 中处理缺失数据的方法：

isna() 和 dropna(): isna() 方法用于检测缺失值，dropna() 方法用于删除包含缺失值的行或列。

import pandas as pd

df = pd.DataFrame({'A': [1, 2, None, 4], 'B': [None, 6, 7, 8]})
df.isna()  # 检测缺失值
df.dropna()  # 删除包含缺失值的行
df.dropna(axis=1)  # 删除包含缺失值的列

fillna(): fillna() 方法用于填充缺失值，你可以指定要使用的值或方法。

df.fillna(value=0)  # 用0填充缺失值
df.fillna(method='ffill')  # 使用前一个非缺失值进行前向填充
df.fillna(method='bfill')  # 使用后一个非缺失值进行后向填充

处理类别数据

这里对类别数据做一个定义：一般以字符串形式出现，表示类别。类别数据分为两种，一种是内在有数值大小关系的，比如衣服尺寸：S，M，L；另一种是标称特征，不具备排序特征。既然是字符串，我们都要处理为数字方便训练。

sklearn

这个函数是处理标签列的，本质上是通过枚举，将所有独立的标签从 0 开始编号。之所以可以这样处理，因为我们不关心类标被赋予哪个整数值。

from sklearn.preprocessing import LabelEncoder
class_le = LabelEncoder()
y = class_le.fir_transform(df['label'].values)

// 如果要将整数类标还原到字符串，可以用：
class_le.inverse_transform(y)

如果是属于特征的类别数据，特别是无序数据，用枚举则是不合适的。这是因为，这会使得模型假定不同类别之间有顺序关系。所以，独热编码更合适。

from sklearn.preprocessing import OneHotEncoder
ohe = OneHotEncoder()
ohe.fit_transform(df['color'].values)

pandas

pandas 有 get_dummies 可以用于实现独热编码

pd.get_dummies(df) // 只对字符串列进行转化

《python机器学习》分类算法

2023年10月2日 · 阅读需 3 分钟

Jason Lee

前言

我打算开一个全新的系列，记录我在学习《python 机器学习》这本书过程中的要点和感想。

决策边界图

分类任务中的一种图，可以看出模型在整个网格内的预测结果。

代码如下：

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.svm import SVC

# 步骤2：加载鸢尾花数据集
iris = datasets.load_iris()
X = iris.data[:, :2]  # 使用前两个特征以便进行可视化
y = iris.target

# 步骤3：训练一个SVM分类器
clf = SVC(kernel='linear')
clf.fit(X, y)

# 步骤4：创建一个网格来覆盖特征空间
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.01), np.arange(y_min, y_max, 0.01))

# 步骤5：对网格上的每个点使用分类器进行预测，获取决策边界
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)

# 步骤6：可视化数据点、决策边界和决策区域
plt.contourf(xx, yy, Z, cmap=plt.cm.Spectral, alpha=0.8)
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Spectral)
plt.xlabel('Sepal Length')
plt.ylabel('Sepal Width')
plt.title('Decision Boundary Visualization')
plt.show()

主要的函数有 meshgrid，功能是生成网格坐标数据。还有 contourf，绘制决策边界图。

逻辑回归

线性计算方式，激活函数采用 sigmoid，从而得出属于正类别的概率。

决策树/随机森林

决策树就是一种二叉树，通过计算一种特征能否尽可能的将类别区分来决定选择哪一种特征作为节点。随机森林则是决策树的集合，通过随机抽样得到训练样本来引入随机性，并且最后由多数投票来确定预测结果。

性能指标（二分类问题）​

混淆矩阵​

准确率和召回率​

ROC 曲线​

PCA（主成分分析）​

LDA（线性判别分析）​

缺失数据值的处理​

在 scikit-learn 中处理缺失数据的方法：​

在 pandas 中处理缺失数据的方法：​

处理类别数据​

sklearn​

pandas​

前言​

决策边界图​

逻辑回归​

决策树/随机森林​

性能指标（二分类问题）

混淆矩阵

准确率和召回率

ROC 曲线

PCA（主成分分析）

LDA（线性判别分析）

缺失数据值的处理

在 scikit-learn 中处理缺失数据的方法：

在 pandas 中处理缺失数据的方法：

处理类别数据

sklearn

pandas

前言

决策边界图

逻辑回归

决策树/随机森林