Jason Lee

每次学习中碰到 k8s，都会被它的复杂性难住。现在网上的教程，要么直接指定 image，省略了 yaml 文件的编写，要么是只有应用节点，没有数据库节点，这就和实际生产环境脱离。所以，我决定自己从头搭建一个集群，整合 Nodejs 和 mysql，打造一个最小示例，作为备忘记录。

这阵子学习《Nodejs 实战》的时候，有看到压力测试的话题，恰好最近工作中也遇到一些高负载场景，所以把这些知识和工具整理出来。

掌握任何一个真实项目，必然要以熟悉编程语言的模块系统为前提。Go 的模块系统有一些独特之处，在这里做一下完整记录。

这篇文章，我打算从 js 有哪些实现计算密集型任务的手段出发，延伸到进程和线程，再到 golang, 从而对并发有一个深刻的认知。

url base64 编码有特殊逻辑。

OOP 在不同编程语言中都通用的概念，并用 js 举例说明，同时包含 ts 相对于 js 独有的特性。

总结一些工作中非常有用的 pgsql 用法。

日期类​

加入 time 列是 timestamp 类型的，那么

需要获得昨日的数据：select ... where time between current_date-1 and current_date;

过去 24 小时：select ... where time > current_timestamp - interval '1 day';

今日的数据：select ... where time > current_date；

过去七天的数据并按天列出：select ... where time > current_date-7 group by extract(day from parking_time)；

需要注意的是，在 where 子句中慎用强转符号::，因为这会让该列索引失效，从而搜索速度变得很慢。应该变通成上面这些形式，即 sql 会在 timestamp 类型和 date 类型比较时自动将 date 类型转为 timestamp 类型。

在 PostgreSQL 中，可以使用不同的函数和模式来将 timestamp 数据类型转换为特定的时间格式。以下是几种常见的方法：

1. 使用 TO_CHAR 函数：TO_CHAR(timestamp, 'format') 函数将 timestamp 转换为指定的时间格式。例如，要将 timestamp 转换为年-月-日 小时:分钟:秒 的格式，可以使用以下代码：

   SELECT TO_CHAR(timestamp_column, 'YYYY-MM-DD HH24:MI:SS') FROM your_table;
   ```
   
   

2. 使用 EXTRACT 函数：EXTRACT(field FROM timestamp) 函数允许提取 timestamp 中的特定时间部分（如年、月、日、小时等）。然后，可以将提取的时间部分按照需要的格式进行拼接。例如，以下代码将 timestamp 转换为年-月-日 格式：

   SELECT EXTRACT(YEAR FROM timestamp_column) || '-' || EXTRACT(MONTH FROM timestamp_column) || '-' || EXTRACT(DAY FROM timestamp_column) FROM your_table;
   ```
   
   

3. 使用 TO_TIMESTAMP 函数和 TO_CHAR 函数的组合：如果要在转换过程中进行一些计算或调整，可以使用 TO_TIMESTAMP 函数将 timestamp 转换为特定格式的时间戳，然后再使用 TO_CHAR 函数将其格式化为字符串。例如，以下代码将 timestamp 转换为带有 AM/PM 标记的小时:分钟:秒 格式：

   SELECT TO_CHAR(TO_TIMESTAMP(timestamp_column), 'HH12:MI:SS AM') FROM your_table;
   ```
   

这些方法只是其中的几种，具体的选择取决于所需的时间格式和转换的要求。可以根据具体情况选择合适的方法。

having 和 where 的区别​

这里有另一种理解方法，WHERE 在数据分组前进行过滤，HAVING 在数据分组后进行过滤。这是一个重要的区别，WHERE 排除的行不包括在分组中。这可能会改变计算值，从而影响 HAVING 子句中基于这些值过滤掉的分组。

性能指标（二分类问题）​

混淆矩阵​

首先，为什么在有准确率（accuracy）的情况下，还要引入别的指标呢？因为受困于数据收集的客观限制，容易出现不平衡问题，比如正类的数量远远大于负类。这样，即使模型将所有样本预测为正类，损失函数也很低，达到了欺骗的效果。因此，我们需要将正类和负类分别的预测结果列出来，如混淆矩阵。

准确率和召回率​

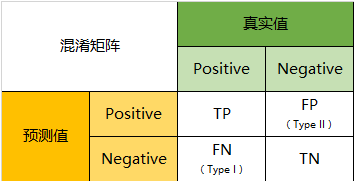
基于混淆矩阵，得到了准确率（precision）和召回率（recall）：

precision = TP/(TP+FP)
recall = TP/(TP+FN)

ROC 曲线​

我们通过真正率（TPR）和假真率（FPR）来衡量分类器的性能。

通过 ROC 空间，我们明白了一条 ROC 曲线其实代表了无数个分类器。那么我们为什么常常用一条 ROC 曲线来描述一个分类器呢？仔细观察 ROC 曲线，发现其都是上升的曲线（斜率大于 0），且都通过点（0,0）和点（1,1）。其实，这些点代表着一个分类器在不同阈值下的分类效果，具体的，曲线从左往右可以认为是阈值从 0 到 1 的变化过程。当分类器阈值为 0，代表不加以识别全部判断为 0，此时 TP=FP=0，TPR=TP/P=0，FPR=FP/N=0；当分类器阈值为 1，代表不加以识别全部判断为 1，此时 FN=TN=0，P=TP+FN=TP, TPR=TP/P=1，N=FP+TN=FP, FPR=FP/N=1。所以，ROC 曲线描述的其实是分类器性能随着分类器阈值的变化而变化的过程。对于 ROC 曲线，一个重要的特征是它的面积，面积为 0.5 为随机分类，识别能力为 0，面积越接近于 1 识别能力越强，面积等于 1 为完全识别。

PCA（主成分分析）​

example:

import numpy as np
from sklearn.decomposition import PCA

# 创建一个示例数据集
data = np.array([
    [1.5, 2.0, 3.0, 4.5],
    [2.2, 2.8, 3.9, 4.2],
    [1.9, 2.5, 3.2, 4.7],
    [2.7, 3.0, 3.6, 4.0],
    [2.3, 2.9, 3.7, 4.3]
])

# 初始化 PCA 模型，指定主成分的数量
pca = PCA(n_components=2)

# 对数据进行拟合
pca.fit(data)

# 获取主成分
principal_components = pca.components_

# 获取主成分的方差贡献比例
explained_variance_ratio = pca.explained_variance_ratio_

# 对数据进行 PCA 转换
transformed_data = pca.transform(data)

print("原始数据：\n", data)
print("主成分：\n", principal_components)
print("主成分的方差贡献比例：", explained_variance_ratio)
print("PCA 转换后的数据：\n", transformed_data)

输出：

原始数据：
 [[1.5 2.  3.  4.5]
 [2.2 2.8 3.9 4.2]
 [1.9 2.5 3.2 4.7]
 [2.7 3.  3.6 4. ]
 [2.3 2.9 3.7 4.3]]
主成分：
 [[-0.61305201 -0.55633419 -0.46392272  0.31533349]
 [-0.53989171 -0.03347232  0.83292811  0.11673604]]
主成分的方差贡献比例： [0.87919714 0.0703791 ]
PCA 转换后的数据：
 [[ 1.00928239 -0.02497259]
 [-0.37705186  0.28493986]
 [ 0.45617665 -0.0677326 ]
 [-0.71873459 -0.2649261 ]
 [-0.36967259  0.07269143]]

在深入之前，有必要解释一下 PCA 为什么在高维数据中找最大方差的方向而不是别的指标（比如最大值），来降维的？找到最大方差的方向意味着在这个方向上数据的变化最为显著，即信息越丰富。以我之前接触到的人脸图像为例，不同位置的像素有差异，才能让分类器有能力识别。

为了将我视频学习到的和这个例子对应起来，将输出中的几个部分进行解释：

首先，这个例子中的原始数据是有五个样本，每个样本有四个维度的特征（一开始我还真没搞明白这个）。然后，pca 算法找出四个主成分（找的过程是通过计算协方差矩阵和特征向量等步骤得来的，视频举的例子是几何平面便于理解，而书上的公式是一种通用的方法，适合任意数量纬度特征，二者本质相同），也就是输出中的主成分。主成分本质上是一个方向向量，且模为 1，所以本例中的主成分有两组，每组四个值，对应四种特征，哪个特征的绝对值最大，说明哪个特征在这个主成分中占主导。方差贡献比例就是，依次计算所有数据在某一主成分上的投影点到距离之和，然后全部求和，最后计算一个主成分所占的比例，比例越高，说明方差越大，数据在这个主成分上差异越明显。最后的转换后数据，则是将所有数据在某一主成分上的投影点到距离，作为以各主成分为新坐标轴的空间内的坐标。

LDA（线性判别分析）​

不同于 PCA，LDA 有类别标签参与训练，所以是有监督的。LDA 训练过程中的优化目标也变成了最大化不同类之间的类间差距，而不是 PCA 的找样本内方差最大的方向，可以说是完全不同的方法，但是都能实现降维。

LDA 在一条线上投影数据点，并且让投影点的不同类之间的均值差距最大，而同类的方差最小，这样就让不同类之间的类间差距最大化。

可以说，LDA 的适用范围更窄些，它要求数据有明确的标签，且只适用分类问题；而 PCA 则适用范围更广，因为它只要求提供特征，能适用于不限于分类的问题。

example:

# 导入必要的库
from sklearn import datasets
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
import matplotlib.pyplot as plt

# 加载示例数据集（这里以Iris数据集为例）
iris = datasets.load_iris()
X = iris.data
y = iris.target

# 创建LDA模型
lda = LinearDiscriminantAnalysis(n_components=2)  # 我们希望将数据降至二维

# 拟合模型并进行降维
X_lda = lda.fit_transform(X, y)

# 绘制降维后的数据
plt.figure(figsize=(8, 6))
colors = ['navy', 'turquoise', 'darkorange']
lw = 2

for color, i, target_name in zip(colors, [0, 1, 2], iris.target_names):
    plt.scatter(X_lda[y == i, 0], X_lda[y == i, 1], alpha=0.8, color=color,
                label=target_name)
plt.legend(loc='best', shadow=False, scatterpoints=1)
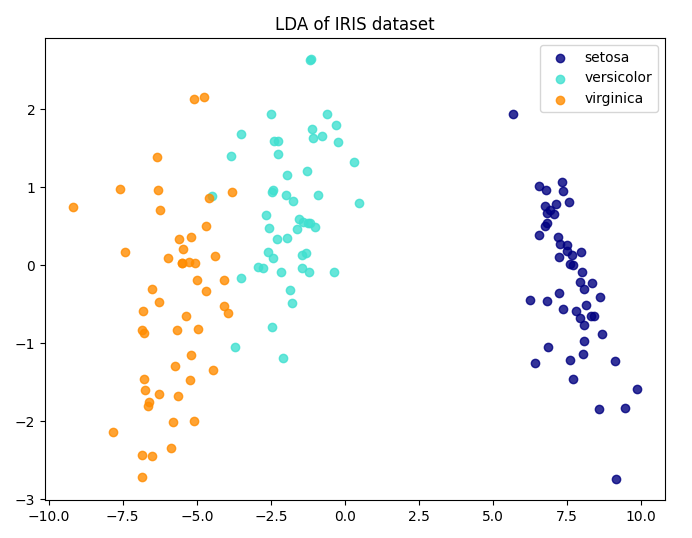
plt.title('LDA of IRIS dataset')
plt.show()

我的工作是后端开发，这几天的内容就是做一套增删改查接口，暂时还没涉及复杂的逻辑。之前在外包里面搞前端，工具就两个：vscode 和浏览器。现在包括但不限于：navicat（操纵数据库）、vscode（写代码）、winscp（把本地写好的代码传到测试服务器）、postman（测试接口）、xshell（查看服务报错日志来 debug）、金山文档（写接口文档）。项目是没有办法在本地运行的，都要上传到测试服务器，通过请求接口后才能知道有无 bug。

之前的一个痛点是，每次写完代码，要在 scp 里面改目录，拖进去；如果每次修改 model、service、controller，就要拖动三次，还容易看错目录，搞得很紧张。后来，自己想的办法是，把 winscp 的文本编辑器由默认的内置改为 vscode，这样，直接从远程服务器上下载一个文件到本地，用 vscode 打开，编辑完保存，改动就同步到服务器上了。